Pascal's Law formula |
||
|
\( \Delta p \;=\; \rho\cdot g\cdot h \) (Pascal's Law) \( \rho \;=\; \dfrac{ \Delta p }{ g \cdot h }\) \( g \;=\; \dfrac{ \Delta p }{ \rho \cdot h }\) \( h \;=\; \dfrac{ \Delta p }{ \rho \cdot g }\) |
||
| Symbol | English | Metric |
| \( \Delta p \) = pressure differential, hydrostatic pressure between two points | \(lbf\;/\;in^2\) | \(Pa\) |
| \( \rho \) (Greek symbol rho) = density | \(lbm\;/\;ft^3\) | \(kg\;/\;m^3\) |
| \( g \) = gravitational acceleration | \(ft\;/\;sec^2\) | \(m\;/\;s^2\) |
| \( h \) = height of liquid column | \(ft\) | \(m\) |
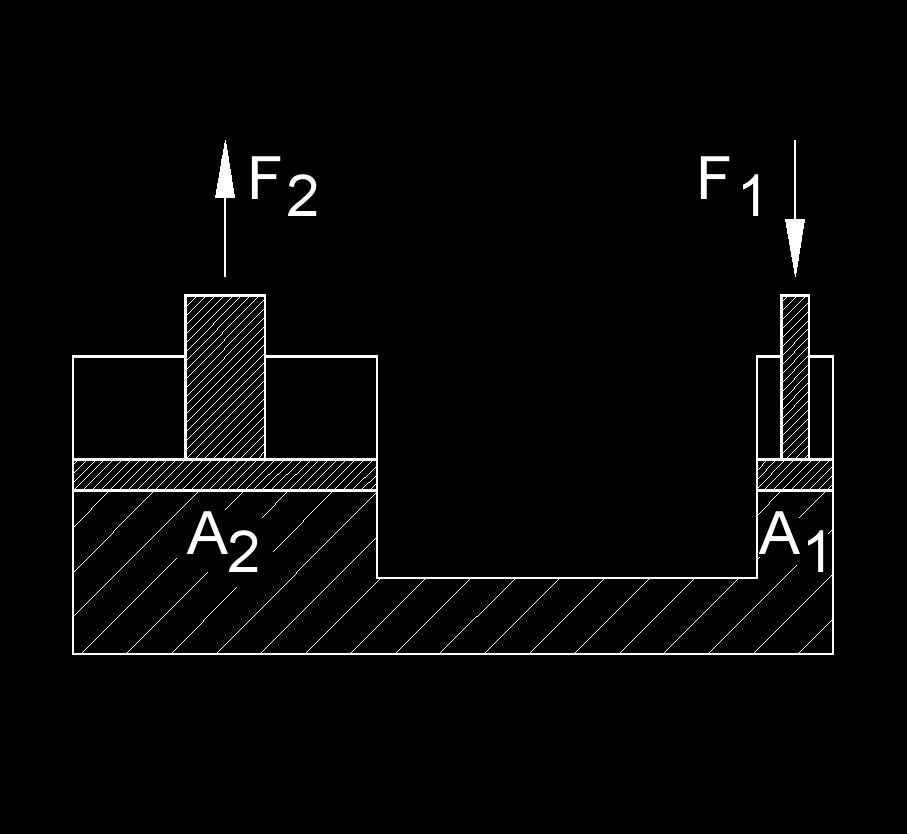
Pascal's law, also called Pascal's principle or the principle of transmission of fluid pressure, states that when there is an increase in pressure at any point in an enclosed fluid, the pressure is transmitted uniformly and undiminished to all portions of the fluid and to the walls of its container. This means that any change in pressure exerted on a fluid in a closed system will be transmitted throughout the fluid, without any loss of pressure, to all parts of the system. This principle is the basis for various practical applications, such as hydraulic systems, hydraulic presses, and hydraulic brakes. In these systems, a small force exerted on a small area can be transmitted and amplified to produce a larger force on a larger area, allowing for mechanical advantage and power amplification.
Pascal's Law has important implications in fluid mechanics and engineering, providing a basis for the design and operation of numerous devices and systems that rely on the transmission of pressure in fluids.
