Cavitation Number
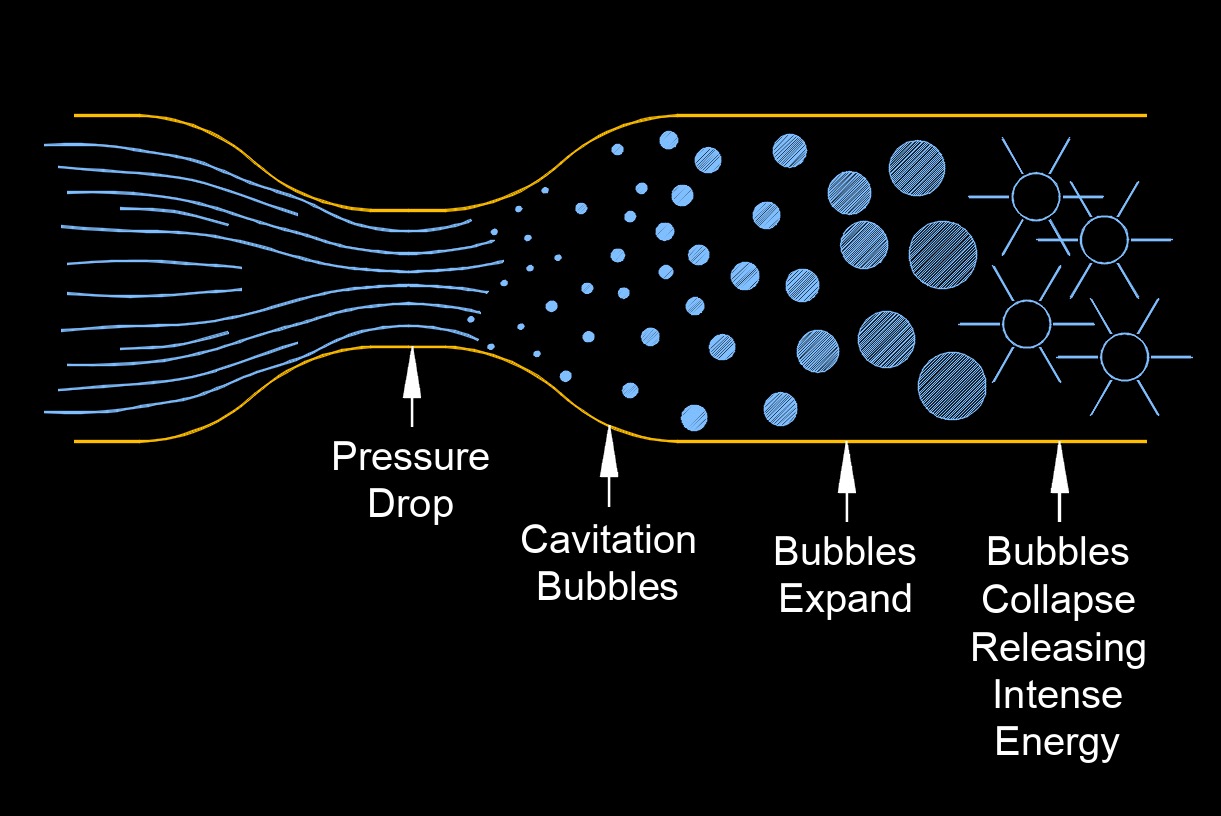
Cavitation number, abbreviated Ca, is a dimensionless number that expresses the relationship between the difference of a local absolute pressure from the vapor pressure and the kinetic energy per volume.
|
\(\large{ Ca = \frac { 2 \left(p \;-\;p_v \right) } {\rho U^2} }\) \(\large{Ca = \frac { \left(p \;-\;p_v \right) } { \frac {1}{2} \rho U^2} }\) Where: \(\large{ Ca }\) = Cavitation number \(\large{ U }\) = characteristic velocity \(\large{ \rho }\) (Greek symbol rho) = density of the fluid \(\large{ p }\) = local pressure \(\large{ p_v }\) = vapor pressure Solve for: \(\large{ p = \frac {Ca \rho U^2} {2} \;+\; p_v }\) \(\large{ p_v = p \;-\; \frac {Ca \rho U^2} {2} }\) \(\large{ \rho = \frac { 2 \left (p \;-\;p_v \right)} {Ca U^2} }\) \(\large{ v = \sqrt { \frac { 2 \left (p \;-\;p_v \right)} {Ca U^2} } }\) |