Compression Formula |
||
| \( \Delta L \;=\; L_f - L_i \) | ||
| Symbol | English | Metric |
| \( \Delta L \) = Change in Length | \( in \) | \( mm \) |
| \( L_f \) = Final Length | \( in \) | \( mm \) |
| \( L_i \) = Initial Length | \( in \) | \( mm \) |
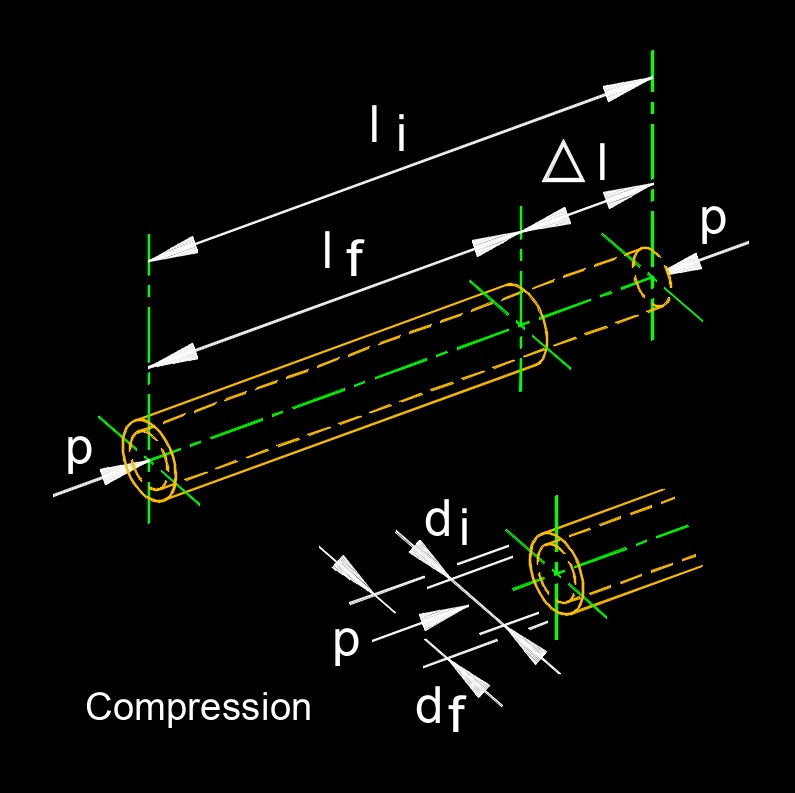
Compression, abbreviated as K, is the force (pressure) acting on a material. Compression is the process of reducing the volume or increasing the density of a substance, typically by applying external forces. It involves the application of pressure to compress or squeeze a material, resulting in a decrease in its volume.
Compression Formulas |
||
|
\( \Delta d \;=\; \epsilon_{di} \cdot d_i \) \( \Delta d \;=\; \dfrac{ \mu \cdot \sigma }{ \lambda } \cdot d_i \) \( \Delta d \;=\; \dfrac{ \mu \cdot p }{ \lambda \cdot A } \cdot d_i \) \( \Delta L\;=\; L_f - L_i \) \( \Delta L\;=\; \lambda \cdot L_i \) \( \Delta L \;=\; \dfrac{ \sigma }{ \lambda } \cdot L_i \) \( \Delta L \;=\; \dfrac{ p }{ \lambda \cdot A } \cdot L_i \) |
||
| Symbol | English | Metric |
| \( \Delta d \) = Change in Depth | \( in \) | \( mm \) |
| \( \Delta L \) = Change in Length | \( in \) | \( mm \) |
| \( A \) = Area | \( in^2 \) | \( mm^2 \) |
| \( \lambda \) (Greek symbol lambda) = Elastic Modulus | \(lbf\;/\;in^2\) | \(Pa\) |
| \( L_f \) = Final Length | \( in \) | \( mm \) |
| \( L_i \) = Initial Length | \( in \) | \( mm \) |
| \( \mu \) (Greek symbol mu) = Poisson's Ratio | \( dimensionless \) | \( dimensionless \) |
| \( p \) = Pressure Under Consideration | \(lbf\;/\;in^2\) | \(Pa\) |
| \( \epsilon \) (Greek symbol epsilon) = Strain | \(in\;/\;in\) | \(mm\;/\;mm\) |
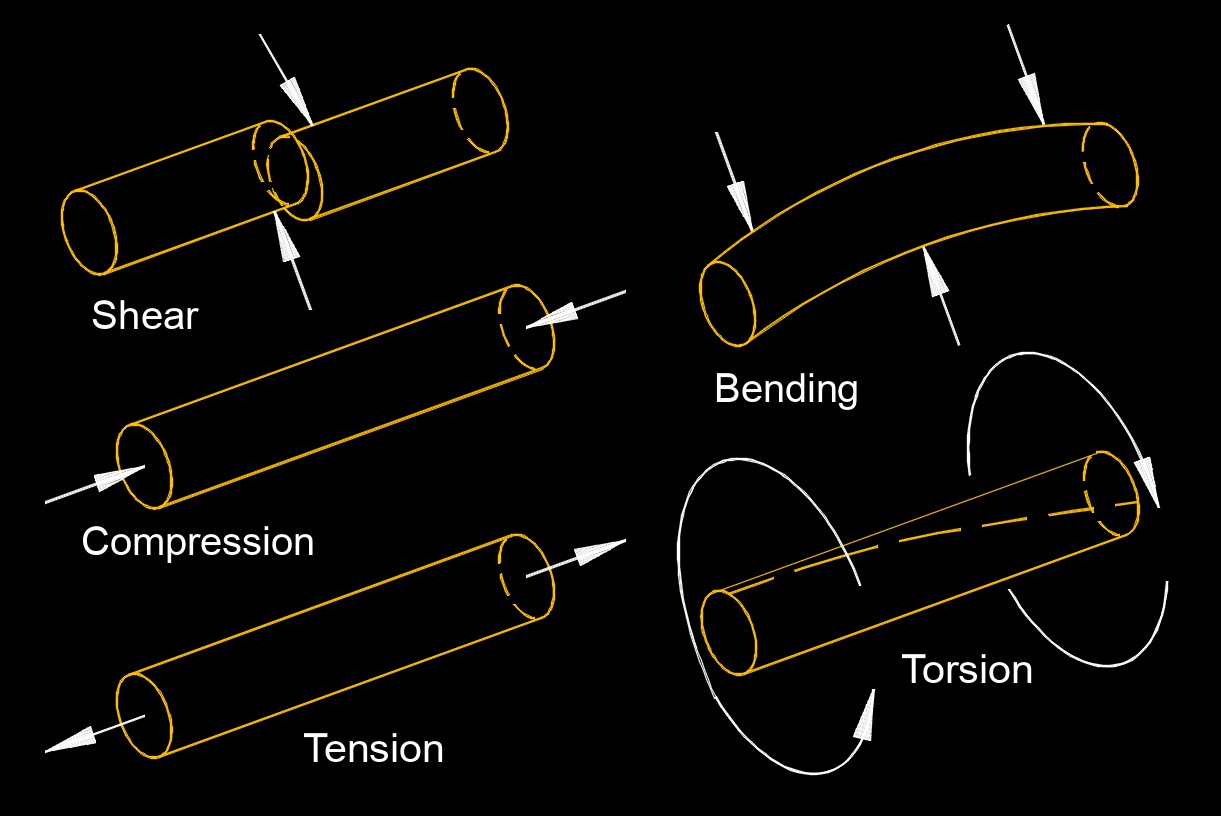Compression is used in physics and engineering. It is used in various applications, including power generation, manufacturing, construction, transportation, and materials science. Understanding the behavior of materials under compression is crucial for designing structures, machines, and systems that can withstand and utilize compressive forces effectively.
