Orifice Area
Orifice Area formula |
||
|
\( A_0 \;=\; \dfrac{ Q }{ C_d \cdot \sqrt{ 2 \cdot G \cdot h_c } }\) (Orifice Area) \( Q \;=\; A_o \cdot C_d \cdot \sqrt{ 2 \cdot G \cdot h_c } \) \( C_d \;=\; \dfrac{ Q }{ A_o \cdot \sqrt{ 2 \cdot G \cdot h_c } }\) \( G \;=\; \dfrac{ \left( \dfrac{ Q }{ C_d \cdot A_o } \right)^2 }{ 2 \cdot h_c }\) \( h_c \;=\; \dfrac{ \left( \dfrac{ Q }{ A_o \cdot C_d } \right)^2 }{ 2 \cdot G }\) |
||
| Symbol | English | Metric |
| \( A_o \) = Orifice Area | \( in^2 \) | \( mm^2 \) |
| \( Q \) = Orifice Flow Rate | \(ft^3 \;/\; sec\) | \(m^3 \;/\; s\) |
| \( C_d \) = Orifice Discharge Coefficient | \( dimensionless \) | \( dimensionless \) |
| \( G \) = Orifice Gravitational Constant | \(lbf-ft^2 \;/\; lbm^2\) | \(N - m^2 \;/\; kg^2\) |
| \( h_c \) = Orifice Center of Head | \( in \) | \( mm \) |
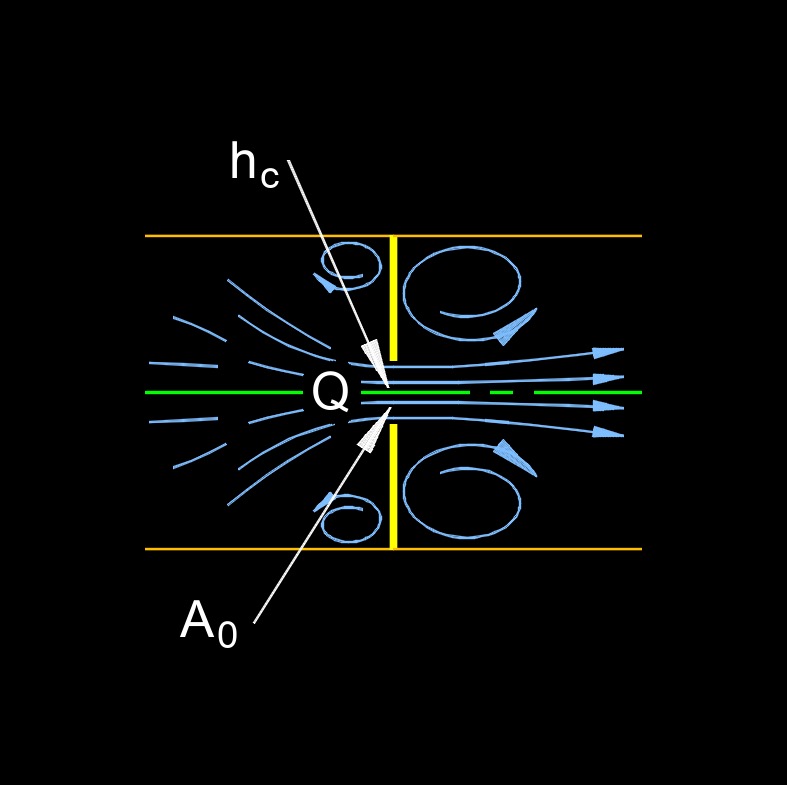
Orifice area is the area cross-section of an orifice, which is a small opening or hole through which fluid flows. The orifice area is an important parameter in fluid dynamics and flow calculations, particularly in applications such as pipes, nozzles, and valves.
- Geometric Orifice Area (GOA) - The orifice opening
- Effective Orifice Area (EOA) - The minimal cross-section area of the downstream jet.
- Contraction Coefficient (\(C_c\)) - The ratio of the area measured at the vena contracta (EOA), to the area of the orifice (GOA) or \(C_c = EOA \;/\; GOA\)
- Discharge Coefficient (\(C_d\)) - The ratio of actual flow to ideal flow or \(C_d = Q_a \;/\; Q_i\)

