Deformation

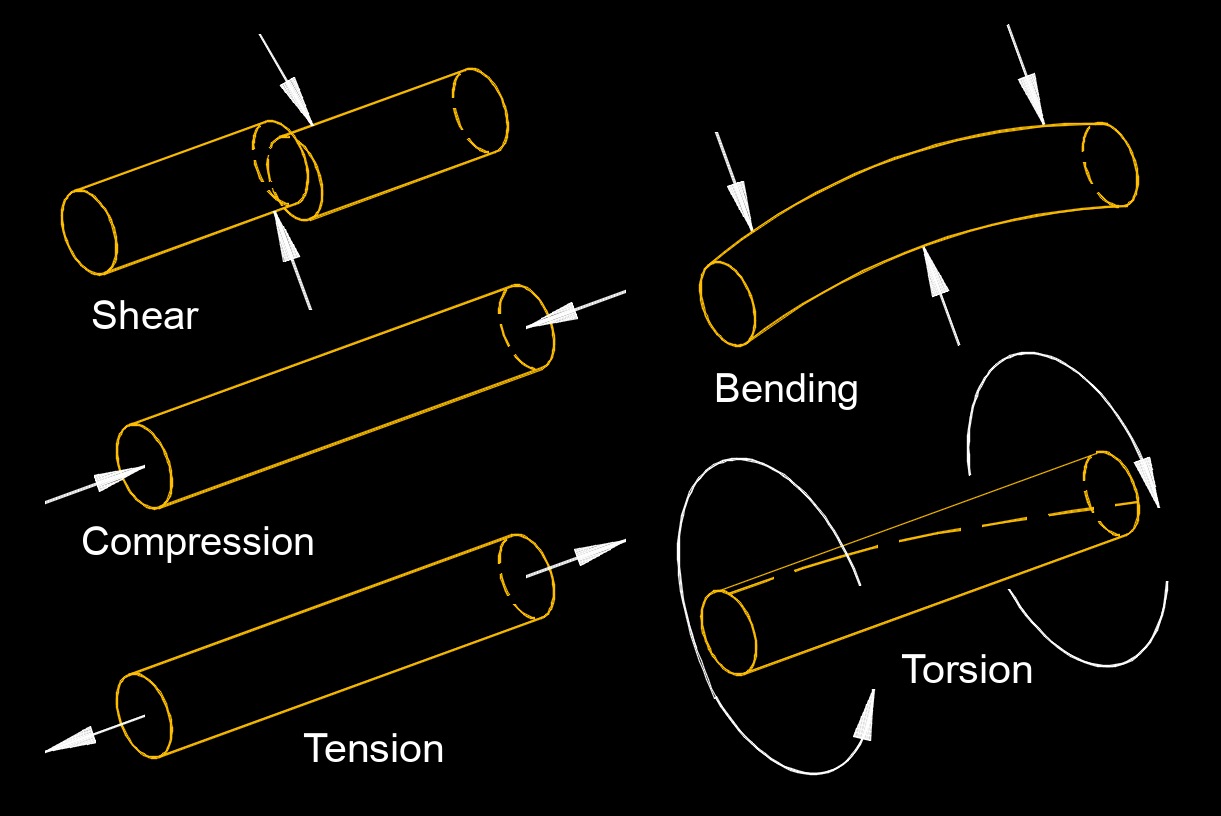Deformation, abbreviated as \( \delta\)  (Greek symbol delta), is measured by how much an object is deformed from its origional dimensions.  Deformation refers to the change in shape, size, or dimension of a material when subjected to external forces or loads.  It is a response of a material to the applied stress, resulting in a change in its physical appearance or structure.

Deformation behavior depends on various factors, including the material's composition, crystal structure, temperature, strain rate, and the nature of applied forces.  Understanding deformation is crucial in engineering and materials science, as it affects the design, performance, and failure analysis of structures and components.  Engineers analyze and predict deformation using mathematical models, stress-strain curves, and experimental techniques such as tensile testing, compression testing, or finite element analysis.

 

 

Deformation Formula
\( \delta \;=\; F_a \; l_i \;/\; A_c \; \lambda \)     (Deformation) \( F_a \;=\; \delta \; A_c \; \lambda  \;/\; l_i \)  \( l_i \;=\; \delta \; A_c \; \lambda  \;/\; F_a \)  \( Ac \;=\; F_a \; l_i \;/\; \delta \; \lambda \)  \( \lambda \;=\; F_a \; l_i \;/\; \delta \; A_c \)
Symbol	English	Metric
\( \delta \)  (Greek symbol delta) = Deformation	\(in\)	\(mm\)
\( F_a \) = Applied Force	\(lbf\)	\(N\)
\( l_i \) = Initial Length	\(ft\)	\(m\)
\( A_c \) = Area Cross-section	\(in^2\)	\(mm^2\)
\( \lambda \)  (Greek symbol lambda) = Elastic Modulus	\(lbf\;/\;in^2\)	\(Pa\)