Elongation

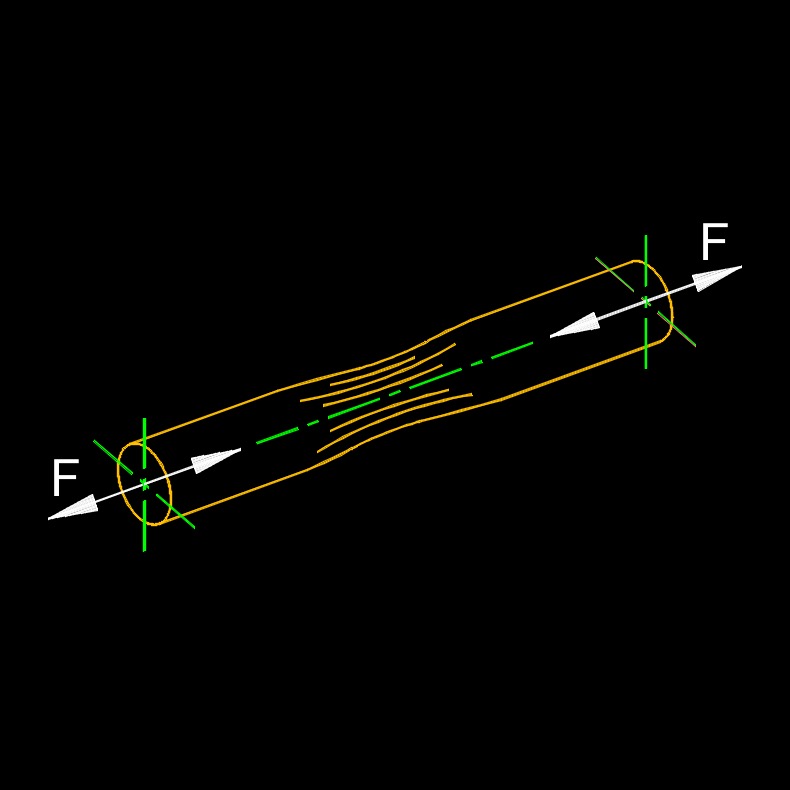Elongation, abbreviated as E, is the increase in length or extension of a material or object when subjected to tensile (pulling) stress.  It is a measure of the deformation that occurs along the axis of the applied force.  Elongation is typically expressed as a percentage and is a critical mechanical property used to assess the ductility or malleability of a material.  When a material is subjected to tension, its atoms or molecules tend to align along the direction of the applied force, causing it to elongate.  The extent of elongation is influenced by the material's composition, structure, and processing.

Elongation is an essential consideration in various industries, such as manufacturing, engineering, and construction, as it indicates how much a material can stretch before it reaches its breaking point.  Ductile materials, characterized by high elongation values, can undergo significant deformation before failure, making them suitable for applications where toughness and flexibility are required.  In contrast, brittle materials have low elongation values and tend to fracture with little or no plastic deformation.

By measuring elongation, engineers and manufacturers can select appropriate materials for specific applications and ensure structural integrity and safety in various products and structures.

 

Elongation Formula
\( E =  F_a \; l_i \;/\; A_c \; \lambda\)     (Elongation) \( F_a =  E \; A_c \; \lambda  \;/\; l_i \)  \( l_i = E \; A_c \; \lambda  \;/\; F_a \)  \( A_c =  F_a \; l_i \;/\; E \; \lambda\)  \( \lambda =  F_a \; l_i \;/\; E \; A_c \)
Symbol	English	Metric
\( E \) = Elongation	\(in\)	\(mm\)
\( F_a \) = Applied Force	\(lbf\)	\(N\)
\( l_i \) = Initial Length	\(in\)	\(mm\)
\( A_c \) = Area Cross-section	\(in^2\)	\(mm^2\)
\( \lambda \)  (Greek symbol lambda) = Elastic Modulus	\(lbf\;/\;in^2\)	\(Pa\)