Bernoulli's Principle

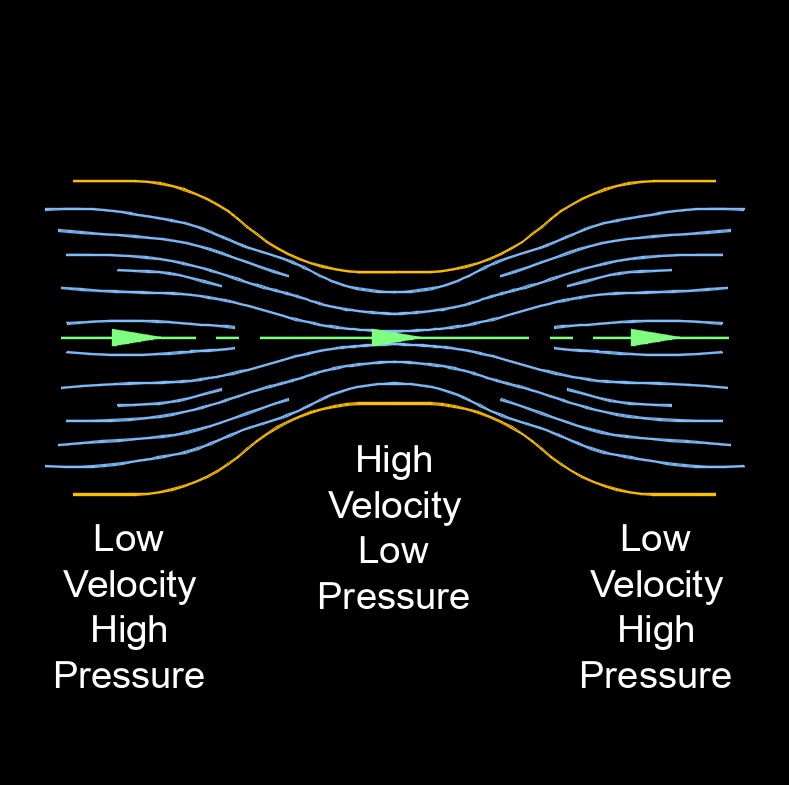
Bernoulli's principle is a principle in fluid dynamics that relates the speed of a fluid to its pressure and the height of the fluid column.  It states that within a steady flow of an incompressible fluid, the sum of the pressure energy, kinetic energy, and potential energy per unit volume remains constant.

Another explination is, the principle states that as the velocity of a fluid increases, the pressure it exerts decreases, and vice versa.  This principle is based on the conservation of energy along a streamline in a fluid flow.  It implies that as a fluid speeds up (increasing its kinetic energy), the pressure it exerts decreases (reducing its potential energy).

These Assumptions Must be Met for the Bernoulli's Equation

• The fluid must be incompressible, even though pressure varies, the density must remain constant.
• The streamline must not enter the boundary layer.  (Bernoulli's equation is not applicable where there are viscous forces, such as in the boundary layer.)

Bernoulli's principle finds applications in various fields, including aerodynamics, hydrodynamics, and fluid dynamics.  It helps explain phenomena such as lift on an airplane wing, the flow of fluids through pipes, the operation of Venturi tubes, and the behavior of fluid in constrictions or around obstacles.  It's important to note that Bernoulli's principle assumes idealized conditions, such as the absence of viscosity, steady flow, and incompressibility of the fluid.  In real world situations, additional factors and phenomena may need to be considered to accurately describe and analyze fluid flow.

static pressure + dynamic pressure + hydrostatic pressure = constant

\( p  + \frac {\rho}{2} \; v^2  + \rho \;g \; h \;=\; constant \)  (along a streamline)     (Bernoulli's Equation)

\( p  + \frac {1}{2} \; \rho\; v^2  + \rho \;g \; h \;=\; constant \)  (along a streamline)

pressure energy + kinetic energy + potential energy = constant

 

Bernoulli's Equation for Pressure
\( p  + (\rho\;/\;2) \; v^2  + \rho \;g \; h \;=\; constant \)     (Bernoulli's Equation for Pressure) \( k \;=\; h \; g \; \rho + v^2 \; (\rho \;/\; 2) + p  \)     (Bernoulli's Equation for Pressure) \( h \;=\;   k - p \;/\; g \; \rho + v^2 \; ( \rho \;/\; 2 )   \) \( g \;=\; k - v^2 \; ( \rho \;/\; 2 ) - p \;/\; h \; \rho    \) \( \rho \;=\; k - p \;/\; h \; g \;  ( 1 + v^2 \;/\; 2 )    \) \( v \;=\; \sqrt{  2 \; ( k - h \; g \; \rho - p )   \;/\; \rho  }   \) \( p \;=\; k - h \; g \; \rho - v^2 \; (\rho \;/\; 2)   \)
Symbol	English	Metric
\( k \) = Constant Pressure	\(lbf\;/\;in^2\)	\(Pa\)
\( h \) = Fluid Column Height	\( ft \)	\( m \)
\( g \) = Gravitational Acceleration	\(ft\;/\;sec^2\)	\(m\;/\;s^2\)
\( \rho \)  (Greek symbol rho) = Fluid Density	\(lbm\;/\;ft^3\)	\(kg\;/\;m^3\)
\( v \) = Fluid Velocity	\(ft\;/\;sec\)	\(m\;/\;s\)
\( p \) = Fluid Pressure	\(lbf\;/\;in^2\)	\(Pa\)

 

Bernoulli's Equation for Energy
\( ( p \;/\; \rho ) + ( v^2\;/\;2 ) + g \; h \;=\; constant \)     (Along a Streamline)
Symbol	English	Metric
\( k \) = Constant Energy	\( lbf-ft \)	\(J\)
\( h \) = Fluid Column Height	\( ft \)	\( m \)
\( g \) = Gravitational Acceleration	\(ft\;/\;sec^2\)	\(m\;/\;s^2\)
\( v \) = Fluid Velocity	\(ft\;/\;sec\)	\(m\;/\;s\)
\( p \) = Fluid Pressure	\(lbf\;/\;in^2\)	\(Pa\)
\( \rho \)  (Greek symbol rho) = Fluid Density	\(lbm\;/\;ft^3\)	\(kg\;/\;m^3\)

 

Bernoulli's Equation for Head
\( ( p \;/\; \rho\;g )  + ( v^2\;/\;2 \;g ) +  h \;=\; constant \)     (Along a Streamline)
Symbol	English	Metric
\( k \) = Constant Head	\( ft \)	\( m \)
\( h \) = Fluid Column Height	\( ft \)	\( m \)
\( v \) = Fluid Velocity	Fluid	\(m\;/\;s\)
\( g \) = Gravitational Acceleration	\(ft\;/\;sec^2\)	\(m\;/\;s^2\)
\( p \) = Fluid Pressure	\(lbf\;/\;in^2\)	\(Pa\)
\( \rho \)  (Greek symbol rho) = Fluid Density	\(lbm\;/\;ft^3\)	\(kg\;/\;m^3\)