Strain Formula |
||
|
\( \epsilon \;=\; \dfrac{ \Delta L }{ L_i }\) (Strain) \( \Delta L \;=\; \epsilon \cdot L_i \) \( L_i \;=\; \dfrac{ \Delta L }{ \epsilon }\) |
||
| Symbol | English | Metric |
| \( \epsilon \) (Greek symbol epsilon) = Strain | \( dimensionless \) | \( dimensionless \) |
| \( \Delta L \) = Change in Length | \( ft \) | \( m \) |
| \( L_i \) = Initial Length | \( ft \) | \( m \) |
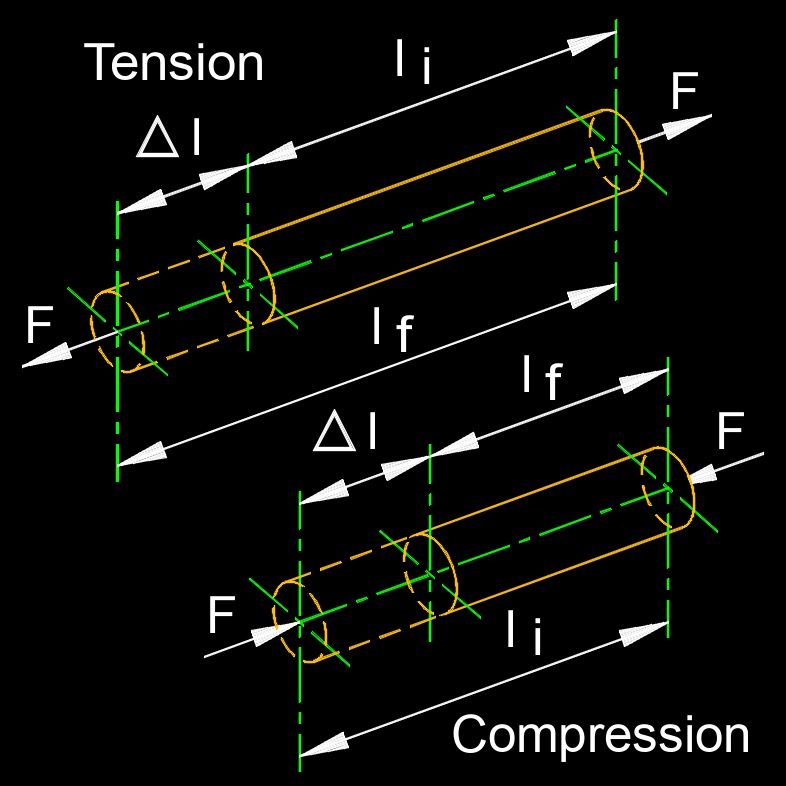Strain, abbreviated as \(\epsilon\) (Greek symbol epsilon), technilly a dimensionless number (but commonly expressed in several ways to indicate the scale of deformation), also called linear strain or longitudinal strain, is a measure of the deformation or elongation experienced by a material when subjected to an external force or load. It quantifies the relative change in size or shape of an object compared to its original size or shape.
Engineers and designers use strain data to understand how materials respond to loads, helping them design structures and components with the right level of elasticity and durability. Additionally, strain measurements are crucial in stress analysis to ensure the safety and performance of various products and systems.
