Nomenclature & Symbols for Engineering, Mathematics, and Science
Engineering, Nomenclature and Symbols, Physics, Mathematics, Science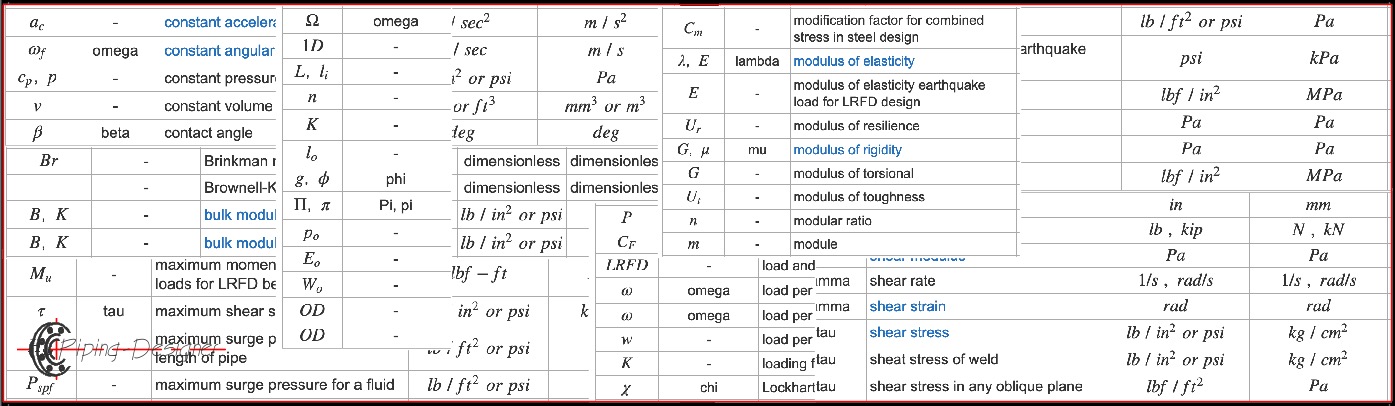
Formula nomenclature is a system of names or terms represented by letters and the Greek alphabet assigned to represent equation physical quantities. Definition symbols vary widely and do not necessarily represent the information being presented the way an abbreviation does. These alphabetical lists contain symbols, greek symbols, definitions, US units, metric units, dimensionless numbers, constants, and constant values.
- See Articles - List of Tags / List of Categories / List of Articles / List of Glossaries / Nomenclature and Symbols
| Physics |
Mathematics and Management Rules and Symbols
Nomenclature & Symbols for Engineering, Mathematics, and Science
- A - B - C - D - E - F - G - H - I - J - K - L - M - N - O - P - Q - R - S - T - U - V - W - X - Y - Z
Nomenclature & Symbols for Accounting, Business, and Finance
- A - B - C - D - E - F - G - H - I - J - K - L - M - N - O - P - Q - R - S - T - U - V - W - X - Y - Z

