Venturi Meter Flow Rate Formula |
||
|
\( Q \;=\; A_2 \cdot \sqrt{ \dfrac{ 2 \cdot ( p_1 - p_2 ) }{ \rho \cdot \left( 1 - \left( \dfrac{ A_2}{A_1} \right)^2 \right) } } \) |
||
| Symbol | English | Metric |
| \( Q \) = Flow Rate | \(ft^3\;/\;sec\) | \(m^3\;/\;s\) |
| \( A_1 \) = Area 1 | \(in^2\) | \(mm^2\) |
| \( A_2 \) = Area 2 | \(in^2\) | \(mm^2\) |
| \( p_1 \) = Fluid Pressure 1 (psi) | \(lbf\;/\;in^2\) | \(Pa\) |
| \( p_2 \) = Fluid Pressure 2 (psi) | \(lbf\;/\;in^2\) | \(Pa\) |
| \( \rho \) = Fluid Density | \(lbm\;/\;ft^3\) | \(kg\;/\;m^3\) |
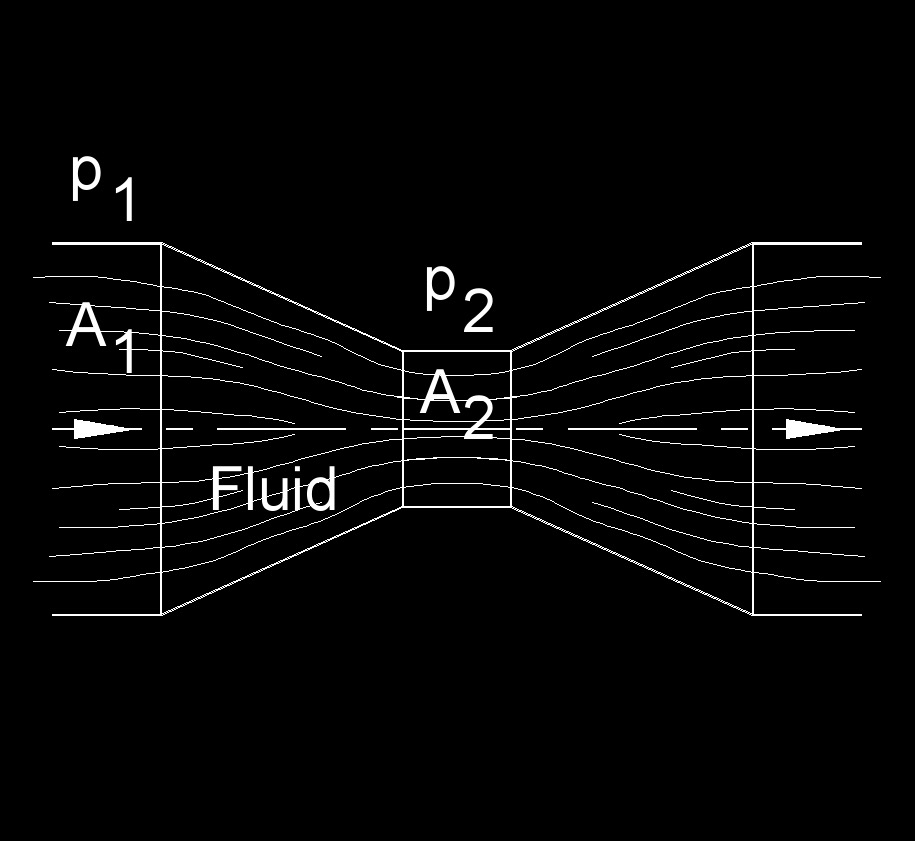Venturi meter is a device used to measure the flow rate of a fluid (liquid or gas) in a pipeline. It operates on the principle of Bernoulli's equation, which relates the velocity of fluid flow to changes in pressure. Venturi meters are commonly used in various industries, including petroleum, water treatment, industrial processes, and HVAC systems, to measure and control fluid flow rates. They are known for their accuracy and reliability in measuring flow.
- See Article - Bernoulli's Equation
Key Points about Venturi Meter Flow Rate
Constriction - A Venturi meter consists of a tube with a gradual constriction in the middle. The fluid flows through this tube. The constriction causes the fluid to accelerate as it passes through the narrow throat of the Venturi meter.
Pressure Difference - According to Bernoulli's equation, as the fluid accelerates in the narrow throat, its velocity increases, and its pressure decreases. Conversely, as the fluid exits the constriction and enters the wider portion of the tube, its velocity decreases, and its pressure increases.
Pressure Measurements - Pressure taps are placed at specific locations in the Venturi meter, typically upstream of the constriction and at the throat. These taps are connected to pressure gauges or transducers to measure the pressure difference between the two points.
Flow Rate Calculation - The flow rate through the Venturi meter can be calculated using the pressure difference between the upstream and throat locations, along with the known properties of the fluid (density and specific gravity), and the Venturi meter's geometry. The flow rate equation is derived from Bernoulli's equation and the principles of fluid dynamics.
